|
 |
- Search
| Healthc Inform Res > Volume 21(2); 2015 > Article |
Abstract
Objectives
The goal of this report is to present an individual patient's survival estimation curve using the each institution's survival data after Cox proportional hazard analysis.
Methods
The program was developed in three parts: input of basic data from Cox proportional hazard analysis, input of individual patient's covariates, and presentation of individual patient's survival curve. In the first part, the average survival rates with each survival time were entered as the means of covariates using the results of Cox proportional hazard analysis. In the second part, the individual patient's values of each covariate were entered for the calculation of survival estimation. In the third part, the survival curve was displayed according to the input data.
Results
The data of 2,652 breast cancer patients were analyzed. Cox regression analysis was conducted using the covariates of age, tumor size, N stage, and M stage. The individual patient's survival curve was presented using the basic data and covariate factors. In the breast cancer patients, the program presented survival curves according to each patient's age, tumor size, N stage, and M stage. The data of 251 thyroid cancer patients were analyzed by a similar method.
The prognosis of individual cancer patients is import in the clinical setting. Most staging systems are used for this purpose, but they do not present quantitative values. For this reason, computer programs or web-based programs have been reported [1,2,3], but these programs are limited to specific types of cancer.
The Cox proportional hazard model [4] is a nonparametric model, which does not require knowledge of the underlying distribution. It can adjust each covariate by multivariate regression analysis. We can obtain the odds ratios of risk factors that are statistically significant. It also shows the average survival rate during a specific survival time with the mean of covariates. Thus, it is possible to create a survival curve for individual patients using the results of the Cox proportional hazard model.
Several programs to estimate the survival rates of cancer patients have been developed previously. For example, the prognosis of breast cancer could be calculated by Adjuvant! Online [3], the PREDICT tool [5], the Finprog study [6] and CancerMath [7].
In this study, we developed a survival estimation program that is different from previously reported methods. We designed our method of individual survival estimation after Cox proportional hazard analysis and developed a computer program to present an individual patient's survival curve not limited to a specific cancer type using each institution's survival data after Cox proportional hazard analysis.
In the Cox proportional hazards model, the survival function (S) at specific time (t) can be calculated from the cumulative baseline hazard function (Λ), regression coefficient (β), and covariates (z) [8]:
The survival function at the mean of covariates (m) is calculated as,
The cumulative baseline hazard function (Λ) can be calculated by the survival function at the mean of covariates (m):
The program was developed using Delphi 5 (Borland International Inc., Austin, TX, USA) under Microsoft Windows 7 (Microsoft Inc., Redmond, WA, USA). The program was composed of three parts: input of basic data from Cox proportional hazard analysis, input of an individual patient's covariates, and presentation of the individual patient's survival curve (Figure 1). In the first part, the average survival rates with each survival time were input as the mean of covariate using the results of the Cox proportional hazard analysis (Figure 2). The covariates were categorical or continuous variables. In each variable, the name, unit, coefficient, and mean value should be entered. Every categorical variable was converted to a dummy variable, which had a value of 0 or 1. The input data could be saved to a file, and the saved data also could be restored (Figure 3).
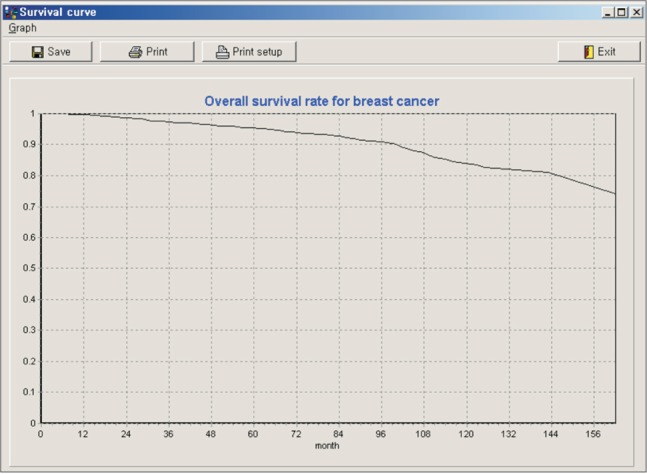
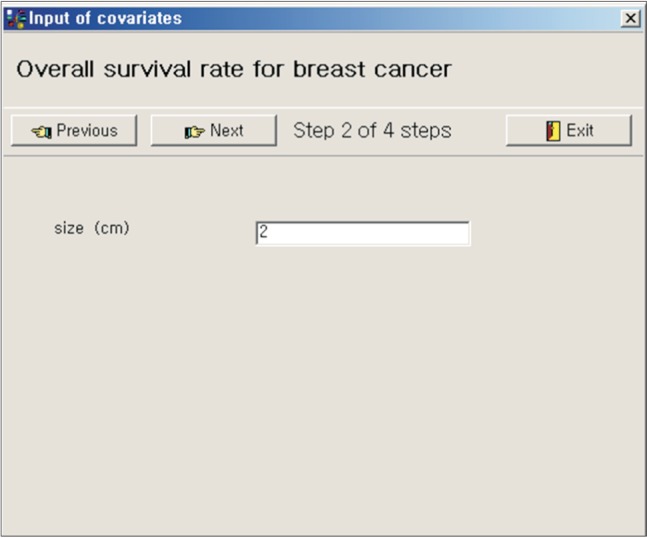
The data of 2,652 breast cancer patients were analyzed using SPSS ver. 19.0 (IBM SPSS Inc., Armonk, NY, USA). Cox regression analysis was conducted using the covariates of age, tumor size, N stage, and M stage. Age and tumor size were continuous variables. N stage and M stage were categorical variables. N stages ranged from 0 to 3 and were converted to dummy variables (N1, N2, N3). The result of analysis showed that each of the 4 covariates was statistically significant. The coefficients and means of covariates and the average survival rates with survival time were entered in the first part of the program (Figures 2 and 3). If we entered a 50-year-old woman with a 2-cm tumor of N1, M0 stage breast cancer (Figure 4), the overall survival curves was like that shown in Figure 5.
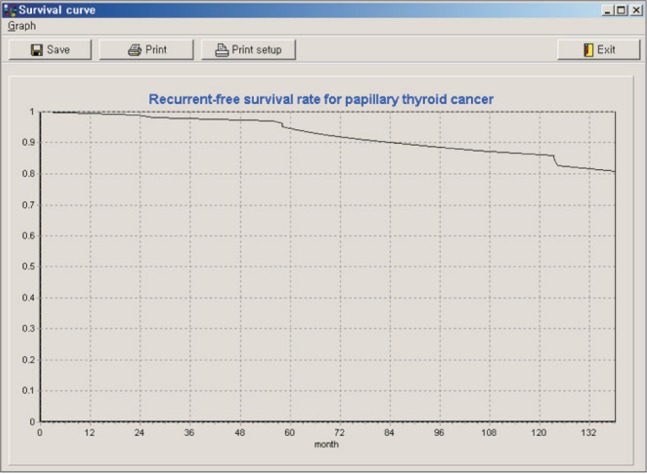
To demonstrate the versatility of the program, we analyzed the recurrent-free survival of 251 thyroid cancer patients. The statistically significant covariates were age, sex, size, extrathyroidal extension, and distant metastasis. The recurrent-free survival curve of a 50-year-old man with a 1-cm tumor, no extrathyroidal extension, and no distant metastasis was like that shown in Figure 6.
The prognosis of cancer differs in Western and Eastern countries. It is assumed that programs of survival estimation developed in western countries are inaccurate for Eastern people. It is also assumed that different institutions have different survival rates. For accurate estimation of survival rates in each institution, it is necessary to develop a program using each institution's own data. In this case report we developed an interactive computer program to present survival estimation curves not limited to one data set but flexible according to the results of Cox regression analysis.
There are many methods to predict the prognosis of cancer [9]. Among these methods, the life table method, the Kaplan-Meier method, and the Cox regression model are most frequently used. All of these three methods are nonparametric models, and the life table method and the Kaplan-Meier method are univariate analyses. In univariate analysis, each of the factors should be analyzed separately, and continuous variables should be converted to categorical variables. If the number of variables increases, the numbers of cases in each category decrease, and the result of analysis will be unsatis factory.
Cox proportional hazard analysis can analyze the continuous variables not converted to categorical variables and can adjust the confounding variables. However, Cox proportional hazard analysis is not more accurate than the Kaplan-Meier method or the life table method. The accuracy of a program depends on the underlying data set, and it is necessary to use accurate data for more accurate prediction.
There have been several programs similar to the one proposed in this paper for specific type of cancer. For example, the prognosis of breast cancer can be calculated by Adjuvant! Online (http://www.adjuvantonline.com), the PREDICT tool (http://www.predict.nhs.uk), the Finprog study (http://finprog.primed.info), and CancerMath (http://www.lifemath.net/cancer/).
Adjuvant! Online displays the 5-year survival rate of individual patients with or without adjuvant treatment, but it does not display the survival curve. It uses an actuarial life table method to calculate survival rates [3]. The PREDICT tool can predict overall survival of breast cancer at 5 and 10 years. It uses a Cox proportional hazard model like this study, but it also does not display survival curves [5]. Finprog displays survival curves like this study, but it uses the Kaplan-Meier method [6]. CancerMath is a series of web-based programs to predict survival of breast cancer, melanoma, and renal cell cancer. It uses the Kaplan-Meier method to display survival curves [7]. The program developed in this report uses Cox proportional hazard analysis to display survival estimation curves. This program has the advantage that it is a universal program not limited to a specific cancer type. Flexible usage is possible by entering the results of Cox proportional hazard analysis.
Although we developed the program using each institution's survival data, we could not validate this program for other institutions. A validation study is needed for clinical application, especially for the other institutions which have different data sets.
In conclusion, we developed a universal interactive program to present individual survival curves of cancer patients. This program will be useful for clinicians to assist their decision-making and discussion with patients.
Acknowledgments
The present research was conducted by the research fund of Dankook University in 2015.
References
1. Esik O, Tusnady G, Daubner K, Nemeth G, Fuzy M, Szentirmay Z. Survival chance in papillary thyroid cancer in Hungary: individual survival probability estimation using the Markov method. Radiother Oncol 1997;44(3):203-212. PMID: 9380818.


2. Wang SJ, Wissel AR, Luh JY, Fuller CD, Kalpathy-Cramer J, Thomas CR Jr. An interactive tool for individualized estimation of conditional survival in rectal cancer. Ann Surg Oncol 2011;18(6):1547-1552. PMID: 21207162.



3. Ravdin PM, Siminoff LA, Davis GJ, Mercer MB, Hewlett J, Gerson N, et al. Computer program to assist in making decisions about adjuvant therapy for women with early breast cancer. J Clin Oncol 2001;19(4):980-991. PMID: 11181660.


4. Lee ET, Wang JW. Identification of prognostic factors related to survival time: Cox proportional hazards model. Statistical methods for survival data analysis. Hoboken (NJ): Wiley; 2003. p. 298-338.

5. Wishart GC, Azzato EM, Greenberg DC, Rashbass J, Kearins O, Lawrence G, et al. PREDICT: a new UK prognostic model that predicts survival following surgery for invasive breast cancer. Breast Cancer Res 2010;12(1):R1PMID: 20053270.



6. Lundin J, Lundin M, Isola J, Joensuu H. A web-based system for individualised survival estimation in breast cancer. BMJ 2003;326(7379):29PMID: 12511459.



7. Michaelson JS, Chen LL, Bush D, Fong A, Smith B, Younger J. Improved web-based calculators for predicting breast carcinoma outcomes. Breast Cancer Res Treat 2011;128(3):827-835. PMID: 21327471.


Figure 1
Overall illustration of program. It is composed of three parts: input of basic data, input of patient's covariates, and display of individual's survival curve.
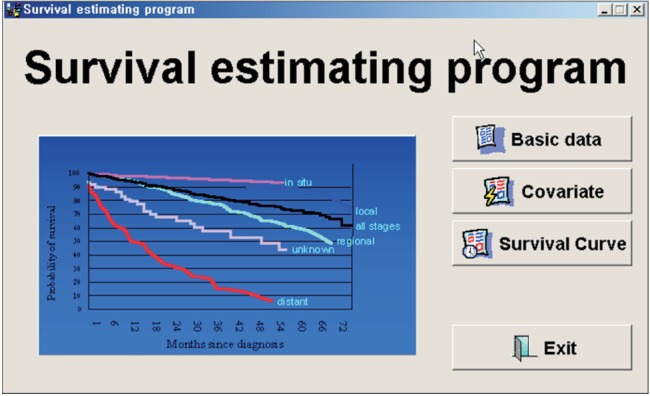
Figure 2
Average survival rates with each survival time were entered as the mean of covariate according to the results of Cox proportional hazard analysis.
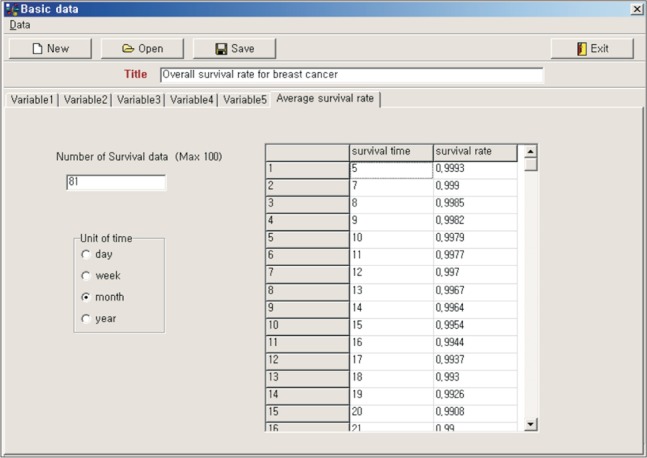
Figure 3
Name, unit, coefficient, and mean value of each covariate were entered for the calculation of survival rate.
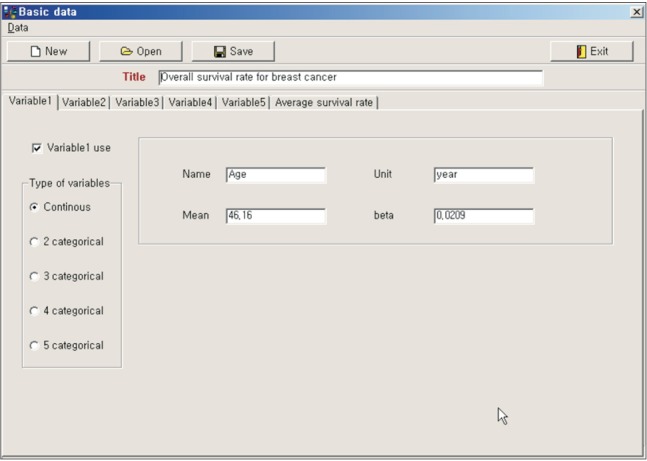
Figure 4
Individual patient's value of each covariate was entered for the calculation of survival rate.
-
METRICS

- Related articles in Healthc Inform Res
-
Development of an Automatic Pill Image Data Generation System2023 January;29(1)