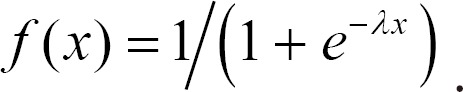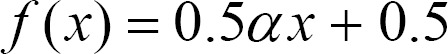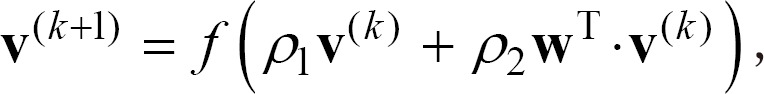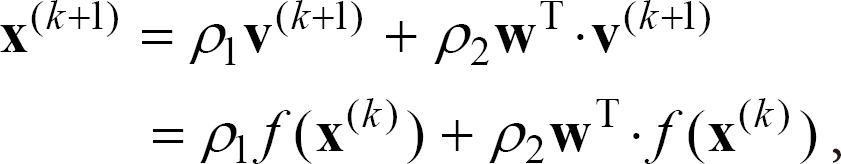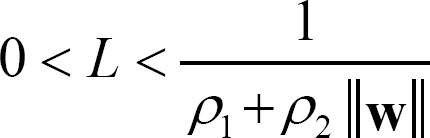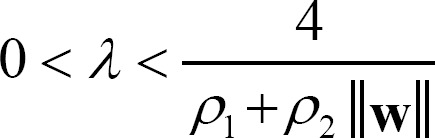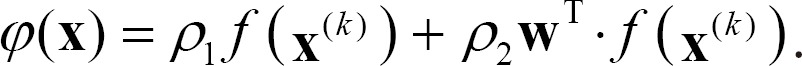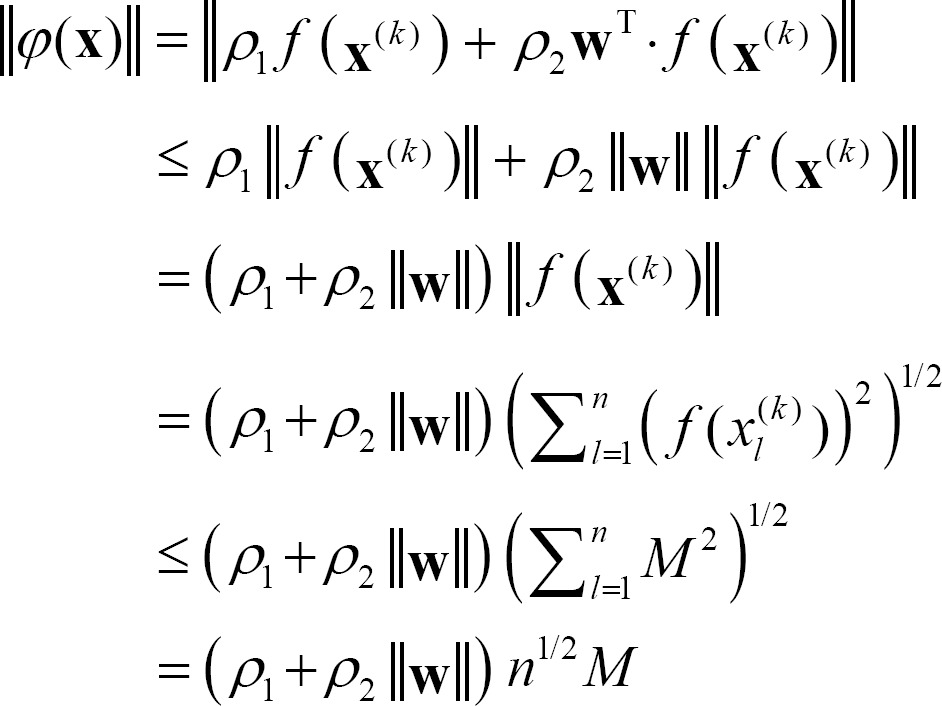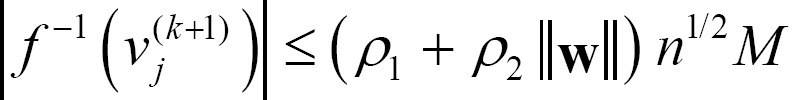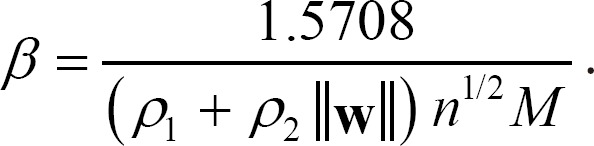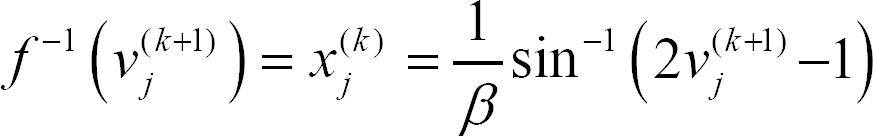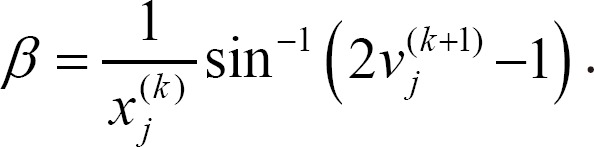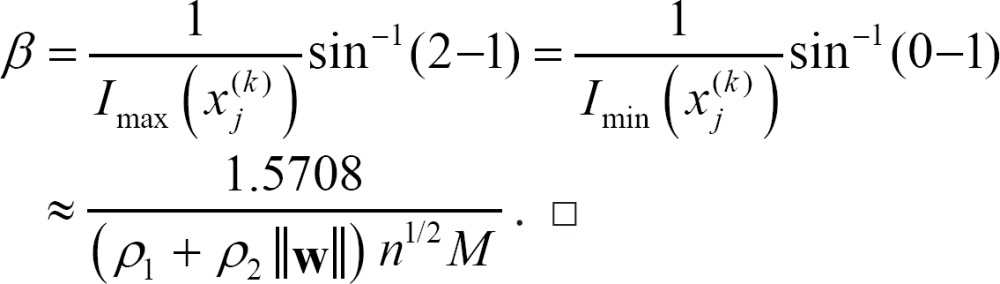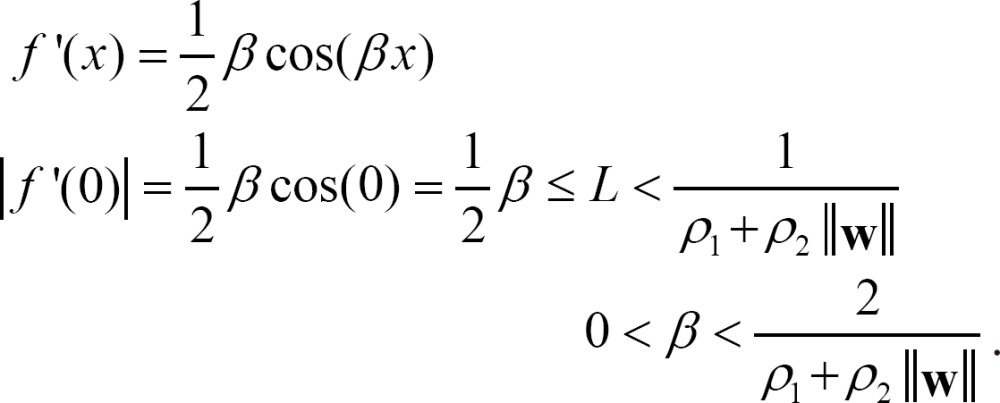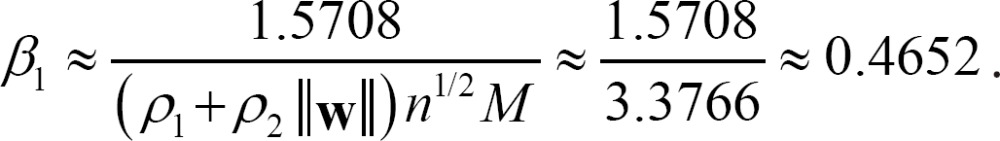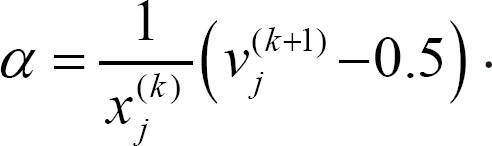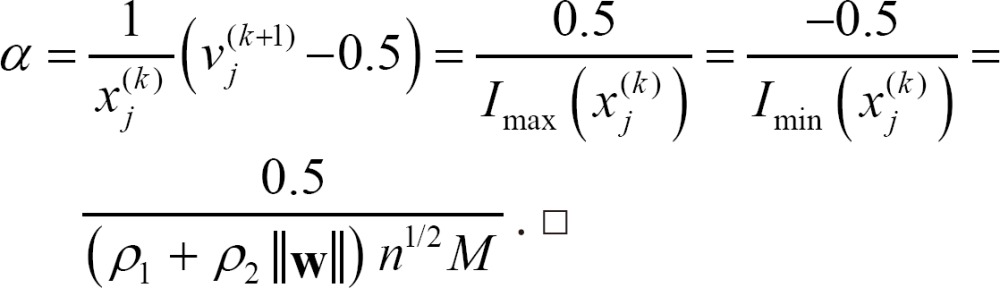I. Introduction
Various artificial intelligence techniques have been used for decision making in medical activities, such as diagnosis and therapy recommendations [1]. However, these techniques can be useful when the physician's knowledge is well represented in terms of computer realization and use. However, a large number of parameters such as medical symptoms and laboratory test results make it difficult for these techniques to be implemented using computers [2]. To overcome this problem, over the past few decades, various methods, e.g., neural networks [3,4], Bayesian networks [5], ontology [6,7], fuzzy cognitive maps (FCMs) [2,8,9], have been proposed to represent a physician's knowledge and to support clinical decision making. In particular, FCMs [2,8-13] can efficiently handle complex modeling problems when assessing clinical decision making tasks [2]. FCMs represent causal knowledge between events and are used as tools that can predict results for current states of events by inference. FCMs have been used in not only clinical decision making but also system control, game theory, information analysis, etc. [10]. The advantages of FCMs are that FCMs can be represented in a matrix form and their inference process involves numerical matrix computations. During the inference process, the value of nodes in FCMs could be out of the range of [0, 1]; therefore, activation functions are used to keep the value of the nodes within the range. Therefore, the activation function used for the inference of FCMs is an important factor in determining the results of the inference.
Several research efforts have been conducted on activation functions for the inference process of FCMs [12-14] where a sigmoid function, hyperbolic tangent function, step function, and threshold linear function have been considered as activation functions, and [13] showed that the sigmoid function offers significantly greater advantages than the other functions. Moreover, Lee and Kwon [12] suggested a method for determining the λ value of a sigmoid function, as shown in Equation (1), to design an activation function that adapts to an FCM model.
During inference, the concept values of FCMs are restricted to v∈(0, 1) by the sigmoid function. One of the characteristics of a sigmoid function is that its domain is (-∞, ∞), whereas the range of the function is (0, 1), i.e., we cannot obtain a "0" or "1" as a concept value after inference. Moreover, while a sigmoid function using λ = 5 [13] is known to be a good degree for normalization in [0, 1], the slope of a function of around χ = 0 is greatly different from that of χ = 1. Therefore, a sigmoid function is not suitable for use as a normalization function.
As shown in Figure 1, the sinusoidal-type function shown in Equation (2) at interval [-βπ/2, βπ/2], and the linear function shown in Equation (3) are better normalization functions than a sigmoid function. Moreover, the range of a sinusoidal-type function is [0, 1], where the domain is restricted to the interval [-βπ/2, βπ/2], and therefore, we can obtain "0" and "1" as the concept values after inference.
II. Methods
1. Model Description and Preliminaries
For convenience, we will use the following notations and definitions throughout this paper.
Notations.
N, R, Rn, and Rn×m denote a set of natural numbers, a real number space, a real n-space, and a set of real n×m matrices, respectively. The superscript "T" denotes a vector and matrix transposition (i.e., if u∈Rn, then uT = [ui]1≤i≤n, and if A=[aij]n×m∈Rn×m, then AT = [aij]m×n, where 1≤i≤n, 1≤j≤m, and n, m∈N). For all u∈Rn, let ∥u∥ denote the Euclidean vector norm (i.e., ∥u∥ = (uT·u)1/2). For all A∈Rn×m, let ∥A∥ denote the spectral norm (i.e., ∥A∥= (the maximum eigenvalue of AT·A)1/2). If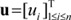 
is a state vector of a system, then 
denotes an equilibrium state vector of the system. If f:R→R, then f'(·) and f-1(·) are the first derivative and inverse function of f(·), respectively. If u∈[u1, u2] for any u, u1, u2∈R, then Imax (u) and Imin (u) stand for the maximum and minimum values of u, respectively, i.e., Imax(u)=u2 and Imin(u)=u1.
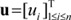is a state vector of a system, then denotes an equilibrium state vector of the system. If f:R→R, then f'(·) and f-1(·) are the first derivative and inverse function of f(·), respectively. If u∈[u1, u2] for any u, u1, u2∈R, then Imax (u) and Imin (u) stand for the maximum and minimum values of u, respectively, i.e., Imax(u)=u2 and Imin(u)=u1.The following descriptions show mathematical models representing the characteristics and inference process of an FCM as defined in [9,12,15].
Definition 1 (Components of FCM). (refer to [15]) Suppose Ci and Cj are concepts in an FCM, and vi and vj are the values of Ci and Cj belonging to [0, 1], respectively, when i, j∈N = {1,2,..., n} and n∈N is the number of concepts. Then, weight wij is defined as a real number in [-1, 1]. We deem the weight as positive, negative, or having no causality from Ci to Cj when wij>0, wij<0, and wij=0, respectively.
Definition 2 (Inference process of FCM). (refer to [15]) For every i∈N and any j∈N, let Ci be the causal concepts that influence concept Cj. Then, for every j∈N and all iteration steps of k≥0 during inference process of the FCM,
where ρ1, ρ2∈(0, 1] and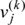 
∈[0, 1] represents the value of Cj at the k -th iteration step. Moreover, f:R→R is an activation function to restrict 
into the interval [0, 1]. Equation (4) is also represented in vector form as
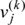∈[0, 1] represents the value of Cj at the k -th iteration step. Moreover, f:R→R is an activation function to restrict into the interval [0, 1]. Equation (4) is also represented in vector form as
where 
and w=[wij]n×n, where 1≤i, j≤n, and are called a state vector and weight matrix, respectively. Moreover, 
.
and w=[wij]n×n, where 1≤i, j≤n, and are called a state vector and weight matrix, respectively. Moreover, .As in [12], we transform the model from Equations. (4) and (5) into the form described in the following definition.
Definition 3 (Transformation). (refer to [12]) For every j∈N and all k≥0, let 
and 
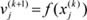in Equation (4); then,
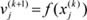and in Equation (4); then,
where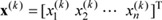 
.
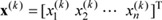.We also consider unipolar, nonlinear, and continuous functions as activation functions of FCMs. Therefore, we assume that the activation functions satisfy the following conditions:
Assumption 1. The function f:R→R is bounded; i.e., 0≤f(u)≤M for all u∈R and any M∈R such that M>0.
Assumption 2. The function f:R→R satisfies the Lipschitz condition with a Lipschitz constant, L > 0; i.e., |f(u1)-f(u2)|≤L|u1-u2| for all u1, u2∈R.
Lee and Kwon [12] suggested a bound of L of activation functions satisfying Assumptions 1 and 2, as shown in Equation (7), which guarantees the global exponential stability of Equation (5) during an inference process of an FCM.
Moreover, as shown in Equation (8), the bound of λ was derived using Equation (7) and the property in which the maximum value of the derivative of a sigmoid function occurs when χ = 0.
Consequently, the λ value are determined by adapting the weight matrix w as an FCM model and the sigmoid function whose λ value satisfies inequality (8) guarantees the stability of Equation (5).
2. Design of Sinusoidal-Type Activation Functions
As mentioned in the introduction, a sinusoidal-type function may not be appropriate to an activation function because it is oscillated in the bound of domain (-∞, ∞). From another viewpoint, the sinusoidal-type function, shown in Equation (2), within the bound of domain [-βπ/2, βπ/2], could be better than a sigmoid function as a normalization function, because a sinusoidal-type function is a monotonous increase function that has a gentler slope than a sigmoid function does. Also, the range of a sinusoidal-type function is [0, 1], which is different than a sigmoid function whose range is (0, 1). Therefore, we need to find the value of β. Intuitively, βπ/2 and -βπ/2 may be the maximum and minimum values that χ can reach during inference, respectively. Consequently, finding the maximum and minimum values of χ is a way to find the value of β. Since a sinusoidal-type function will be used as an activation function for Equation (5) in this paper, the domain values will be the elements of vector v(k) in Definition 3. To find the bound of x(k) as the result of inference of an FCM using Equation (5), we give following lemmas.
Lemma 1. Let x(k) and M be the same as in Definitions 3 and Assumption 1, respectively. Then, for all k≥0 , the following inequality is satisfied.
Proof. Let the right term of inequality (6) be φ(x) as follows:
If we use the Euclidean norm for both terms of Equation (10), we can then derive the following inequality.
Therefore, we have
If we suppose there exists x(-1) such that v(0)=f(x(-1)), then inequality (11) is represented as Equation (9) because of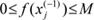 
from Assumption 1. □
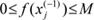from Assumption 1. □
Lemma 2. Let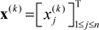 
be the same as in Definition 3. Then, for all 1≤j≤n, 
.
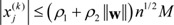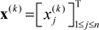be the same as in Definition 3. Then, for all 1≤j≤n, .
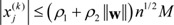Proof. Consider a vector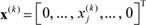 
. Then, 
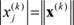. Here, |
| is the maximum absolute value among other elements within the unit circle in the vector norm. Thus, from inequality (11), we have . □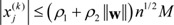
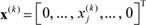. Then, 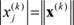. Here, || is the maximum absolute value among other elements within the unit circle in the vector norm. Thus, from inequality (11), we have 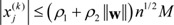. □We can know the domain range of a sinusoidal-type activation function used in the inference process of FCMs through Lemmas 1 and 2. Therefore, we give following theorem for the design of the sinusoidal-type activation function.
Theorem 1. Let 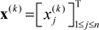and M be the same as in Definition 3 and Assumption 1. If there exists an inverse function, f-1(·), of an activation function, f(·), the following equation is satisfied for all k≥0 and any j∈N.
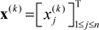and M be the same as in Definition 3 and Assumption 1. If there exists an inverse function, f-1(·), of an activation function, f(·), the following equation is satisfied for all k≥0 and any j∈N.
Proof. If is the j-th element of x(k), by Lemma 2 we know the range of to be 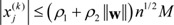. Also, 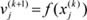can be represented as 
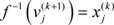because f(·) is invertible. Therefore, we finally have 
. □
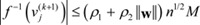is the j-th element of x(k), by Lemma 2 we know the range of to be 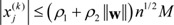. Also, 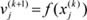can be represented as 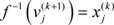because f(·) is invertible. Therefore, we finally have . □
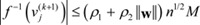Note 1. If we know the range of and for all k≥0 and j∈N, we can design activation functions satisfying Assumptions 1 and 2 by assigning Imax() and Imin() to Imax() and Imin(), respectively.
and for all k≥0 and j∈N, we can design activation functions satisfying Assumptions 1 and 2 by assigning Imax() and Imin() to Imax() and Imin(), respectively.The following corollary shows how to actually design a sinusoidal-type activation function using Theorem 1.
Corollary 1. Let β be the same as in Equation (2) and ρ1, ρ2, w, n, and M be the same as in Theorem 1. Then, in the designed sinusoidal-type activation function, the value of β is
Proof. We can easily derive the following equation, which is the inverse function of Equation (2).
Thus, we have
If Imax() and Imin() are assigned to Imax()=1 and Imin()=0, respectively, then β is computed as
) and Imin() are assigned to Imax()=1 and Imin()=0, respectively, then β is computed as
The following corollary shows that the designed sinusoidal-type activation function guarantees the global exponential stability of the inference process of an FCM.
Lemma 3. (refer to [12]) If is the same as in Definition 3, and L is a Lipschitz constant as shown in Assumption 2, then for all j∈N, |f'()|≤L.
is the same as in Definition 3, and L is a Lipschitz constant as shown in Assumption 2, then for all j∈N, |f'()|≤L.
Corollary 2. The inference process of an FCM using Equation (5) is globally exponentially stable when the activation function is a sinusoidal-type, as in Equation (2), where β=1.5708/(ρ1+ρ2∥w∥)n1/2.
Proof. The sinusoidal-type function of Equation (2) satisfies Assumption 1, and the maximum value of the first derivative of the function occurs when χ=0. Therefore, the range of β is calculated using inequality (7) and Lemma 3 as follows:
This guarantees the global exponential stability of Equation (5). If M = 1 in inequality (13), we finally have
This inequality is satisfied for all n∈N. Therefore, Equation (2), where β=1.5708/(ρ1+ρ2∥w∥)n1/2, also guarantees the global exponential stability of Equation (5). □
We next give an example that confirms the stability of the inference process using the designed sinusoidal-type activation function.
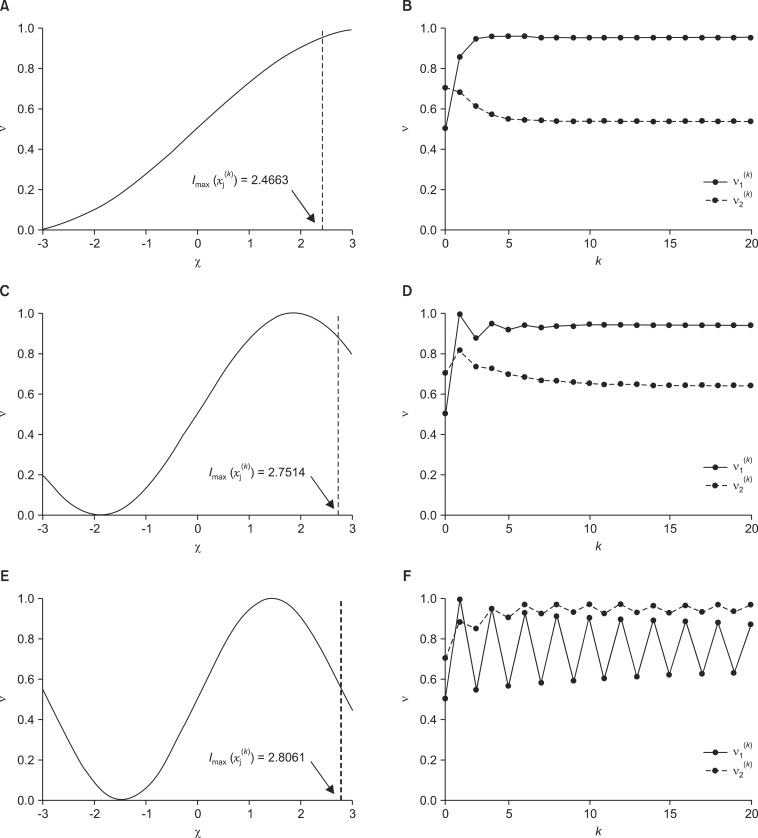
Example 1. Let ρ1=ρ2=1 and M=1 in Definition 2 and Assumption 1. Also, suppose that weight matrix w and initial state vector v(0) are
The following three kinds of sinusoidal-type activation functions with different values of β are considered in this example:
(i) β1 = 0.4652, calculated by the proposed method, where n=2:
(ii) β2=0.8376, which is within the range of β calculated by inequality (14), and guarantees the global exponential stability of the inference process,
0<β<0.83766392031338.
(iii) β3 = 1.0870, which is out of the range of β, and does not guarantee the global exponential stability of the inference process.
Using the designed sinusoidal-type activation functions, the inferences in Equation (5) based on w and v(0) are performed. After inference, the following results are obtained: vectors saturated to (i)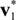 
= [0.9501 0.5346] and (ii) 
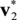= [0.9369 0.6396], and vectors oscillated between (iii) 
= [0.7706 0.9451] and 
= [0.7355 0.9401].
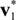= [0.9501 0.5346] and (ii) 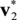= [0.9369 0.6396], and vectors oscillated between (iii) = [0.7706 0.9451] and = [0.7355 0.9401].
Figure 2 shows the designed activation functions and trajectories of the concept values during inference. The results in (i) and (ii) are stable, but some oscillation is observed at the start of the trajectory in the result in (ii), as shown in Figure 2D. Otherwise, the result in (iii) is not stable. Comparing the result in (i) with those in (ii) and (iii), it is reasonable to conclude that this oscillation in the trajectories is caused by the activation functions, which are Imax(f())<||, where j∈{1, 2}.
))<||, where j∈{1, 2}.3. Design of Linear Activation Functions
A linear function, as shown in Equation (3), is not appropriate for an activation function for inference of FCMs, because it monotonously increases for the domain and range of (-∞, ∞). However, if we know the domain range of the linear function to be reached during inference process, we can design the linear function as an activation function. That is, the following corollary shows a way to design a linear-type activation function that satisfies the following condition.
Assumption 3. The function f:R→R is bounded; i.e., 0≤f(u)≤M for all u,u1,u2∈R such that u∈[u1, u2] and u1<u2, and any M∈R such that M>0.
Corollary 3. Let α be the same as in Equation (3) and ρ1, ρ2, w, n, and M be the same as in Theorem 1. Then, in the designed linear-type activation function, the value of α is
Proof. We derive the following equation, which is the inverse function of Equation (3).
Thus, we have
If Imax() and Imin() are assigned to Imax()=1 and Imin()=0, respectively, then α is computed as
) and Imin() are assigned to Imax()=1 and Imin()=0, respectively, then α is computed as
4. Design of FCM on Pulmonary Infection
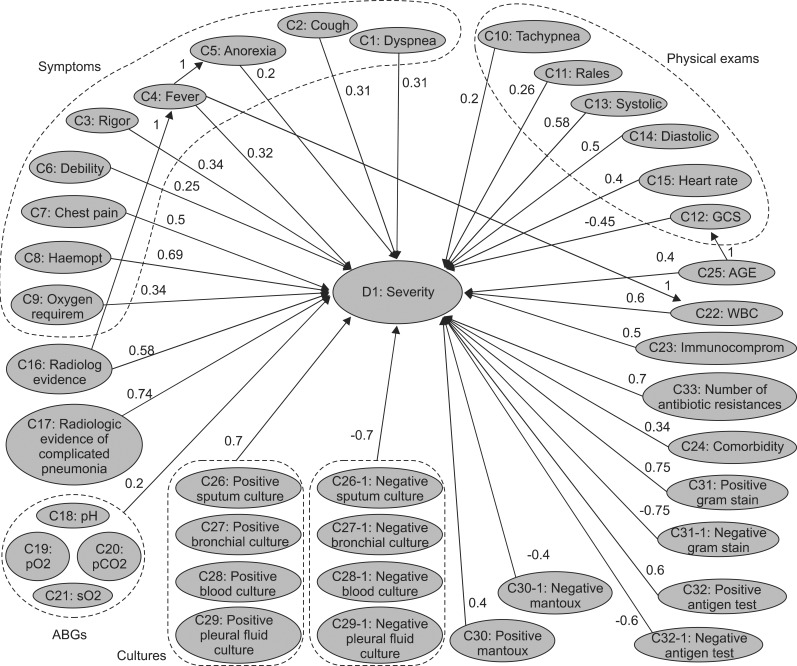
To apply he designed sinusoidal-type and linear activation functions to an FCM model for a clinical decision, we refer the FCM model designed in [2] representing causal knowledge of pulmonary infections. However, the characteristics of the FCM in [2] are different with those of the FCM considered in this paper. That is, different from Definition 1, the concept values in [2] were bounded into the interval [-1, 1], and a bipolar activation function was used for the inference process. Therefore, we customize the FCM model designed in [2], as shown Figure 3, by adding seven concepts (C26-1, C27-1, C28-1, C29-1, C30-1, C31-1, and C32-1) representing the negative values of the concepts (C26, C27, C28, C29, C30, C31, and C32, respectively), as was done in [11]. For instance, if the concept value of C26 is "vC26=-1," then D1 is affected by the amount from vC26×wC26,D1=-1×0.7. However, according to Definition 1, we cannot represent the concept value of "-1." To affect negative influence on D1, we create a new concept, C26-1, which applies a negative value to concept C26, i.e., if "sputum culture" is "-1" then "vC26-1=1" because C26-1 involves the meaning of the negative concept value. Moreover, we give the weight "wC26-1,D1=-0.7" between concepts C26-1 and D1, i.e., even though the value of C26-1 is positive, D1 is affected negatively by vC26-1×wC26-1,D1=1×(-0.7).
We deal with the two scenarios described in [2]. That is, this experiment aims to show the process for physician's decision that which patient is more serious in pulmonary infection, based on observed symptoms and laboratory test results of patients in the following scenarios.
Scenario 1: An immunocompromised patient (A23 = 1) with a high fever (A4 = 0.7), loss of appetite (A5 = 1), and high systolic blood pressure (A13 = 0.7), with radiologic evidence present in his/her chest x-rays (A16 = 1), a small number of WBCs (A22 = 0.4), a negative sputum culture (A26-1 = 1), and negative antigen (A32-1 = 1).
Scenario 2: An older patient (A25 = 0.8) with a low fever (A4 = 0.3), altered mental status (A12 = 0.4), high oxygen requirements (A9 = 0.8), a normal number of leukocytes-white blood cell (A22 = 0), positive sputum culture (A26 = 1), negative blood culture (A28-1 = 1), and negative gram stain (A31-1 = 1).
III. Results
According to [2], physicians made decision that the patient in scenario 1 is more serious in pulmonary infection than that in scenario 2, and the inference of FCM also shows the same result with the physicians' decision. In this experiment, therefore, we compared the results of the inference process of the FCMs with four activation functions, (i) the sigmoid function designed in [12], (ii) a sinusoidal-type function designed using the method proposed in [12], (iii) a sinusoidal-type function and (iv) a linear function designed using the proposed method. In these inferences, we provided the same stimulus as in [16].
According to the two scenarios, we created the following initial state vectors:
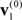=[0 0 0 0.7 1 0 0 0 0 0 0 0 0 0.7 0 1 0 0 0 0 0 0.4 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0],
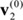=[0 0 0 0.3 0 0 0 0 0.8 0 0 0.4 0 0 0 0 0 0 0 0 0 0 0 0 0.8 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0].
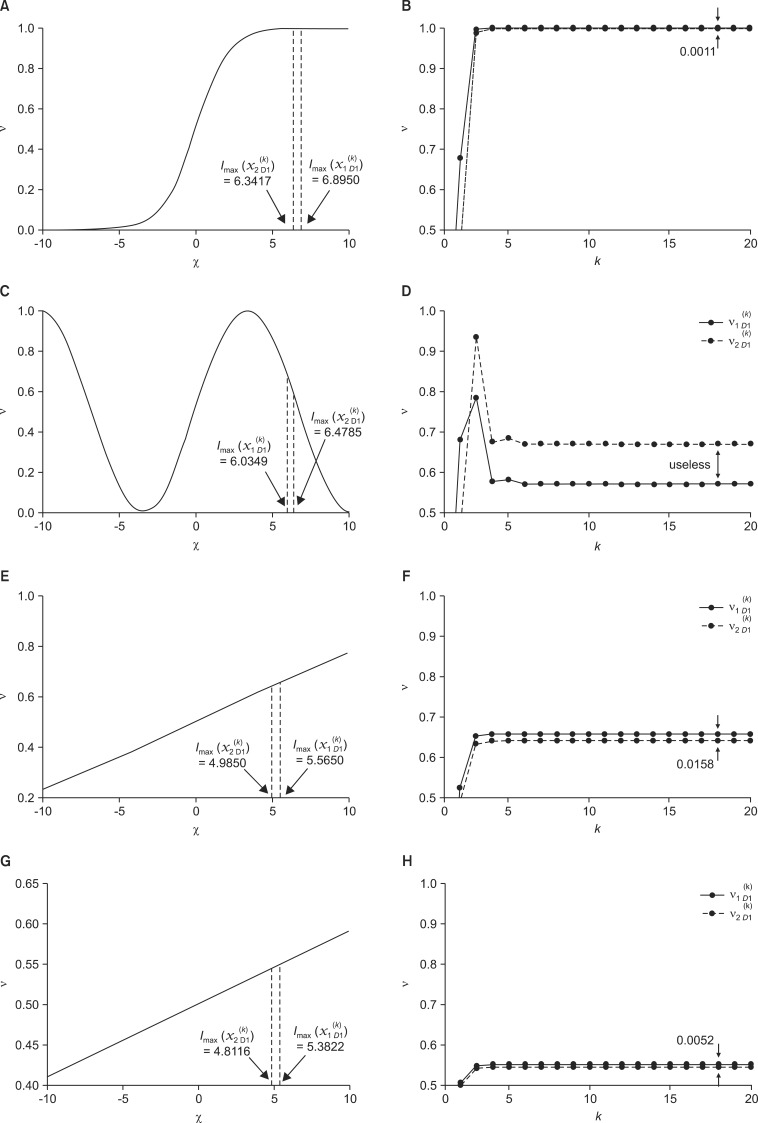
Figure 4 shows the designed activation function and trajectories of the values of concept "D1: Severity" at each inference of the two scenarios.
For (i), the values of concept D1 regarding scenarios 1 and 2 were converged to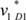 
=0.9983 and 
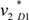=0.9972, respectively. As shown in Figure 4A, the slope is almost flat around the maximum values of 
and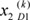 
, and thus the gap between the converged concept values is very small, at |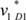-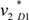|=0.0011. Even though it was difficult to make a decision based on the results in (i), the results showed that the patient in scenario 1 has a severer condition than the patient in scenario 2, which is the same result determined in [2].
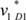=0.9983 and 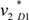=0.9972, respectively. As shown in Figure 4A, the slope is almost flat around the maximum values of and 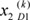, and thus the gap between the converged concept values is very small, at |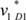-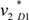|=0.0011. Even though it was difficult to make a decision based on the results in (i), the results showed that the patient in scenario 1 has a severer condition than the patient in scenario 2, which is the same result determined in [2].For (ii), the values of concept D1 regarding scenarios 1 and 2 were converged to 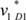=0.5691 and 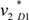=0.6688, respectively. However, in the designed activation function, as shown in Figure 4C, the maximum values of and 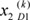exceeded the value that yielded Imax(v). As a result, the patient in scenario 2 has a severer condition than the patient in scenario 1, which is contrary to (i). That is, the result is not useful for decision making.
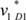=0.5691 and 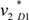=0.6688, respectively. However, in the designed activation function, as shown in Figure 4C, the maximum values of and 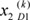exceeded the value that yielded Imax(v). As a result, the patient in scenario 2 has a severer condition than the patient in scenario 1, which is contrary to (i). That is, the result is not useful for decision making.For (iii), the values of concept D1 regarding scenarios 1 and 2 were converged to 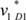=0.6556 and 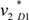=0.6398, respectively. Differing with cases (i) and (ii), the designed activation function looks almost like a linear function around the maximum values of and 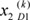. Moreover, the gap between the converged concept values is the largest among the results, at |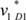-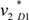|=0.0158. That is, comparing (i) and (iii), we can see that the results of the latter make it more convenient for a physician to make a decision and with more correct results.
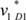=0.6556 and 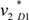=0.6398, respectively. Differing with cases (i) and (ii), the designed activation function looks almost like a linear function around the maximum values of and 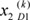. Moreover, the gap between the converged concept values is the largest among the results, at |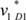-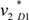|=0.0158. That is, comparing (i) and (iii), we can see that the results of the latter make it more convenient for a physician to make a decision and with more correct results.For (iv), the values of concept D1 regarding scenarios 1 and 2 were converged to 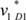=0.5487 and 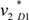=0.5435, respectively. The gap between the converged concept values is the better than the result in (i), at |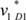-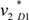|= 0.0052.
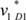=0.5487 and 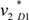=0.5435, respectively. The gap between the converged concept values is the better than the result in (i), at |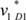-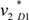|= 0.0052.As a result, we can see that although the sinusoidal-type activation functions was designed using the method proposed in [12], it occasionally provides incorrect results for decision making. Therefore, we can determine that the method proposed in this paper is more appropriate for designing sinusoidal-type activation functions than the method proposed in [12].
IV. Discussion
There exist various methods to support physicians' clinical decision making such as fuzzy, neural networks, decision tree, and FCMs. However, the usability of the methods is strongly dependent on the features of a clinical field; because their knowledge models are different from each other and each method has its own strength and weakness. And even in the same method, the results of decision making may be different according to its knowledge model. Thus, the users in clinical field (e.g., physicians) only refer to the results from the methods when they make clinical decisions. The aim of the methods in clinical field is how clearly shows the results to the users.
In this paper, we focused on a clinical decision making based on FCMs, which are good models of the causal knowledge of relationships between medical concepts and provide prediction results based on the current status of a concept through an inference process. Therefore, activation functions used for the inference process are very important factors that support physicians in making the right decision. In other words, for physicians to make a final decision, how well the physicians' knowledge is represented as an FCM model is not the only important factor. The inference process of that model is also important in the application of clinical decision making. In general, sigmoid functions have been used as activation functions for the inference process of FCMs; the design of an activation function is greatly dependent on the experience of experts because, during inference, the slope varies considerably within the domain range of the function.
Therefore, we proposed a method for designing sinusoidal-type and linear activation functions by calculating the domain range of the activation function to be reached during the inference process of FCMs. Even though sinusoidal-type functions are oscillated and linear functions are monotonously increased within the entire range of the domain, the designed activation functions make the inference stable because the proposed method notices where the function is used in the inference. Moreover, because a sinusoidal-type function designed by the proposed method provides a gentler slope than a sigmoid function does, it can be used as a normalization function. We applied the designed functions to an FCM model that represents the causal knowledge of pulmonary infections. Comparing the activation function designed using the proposed method with activation functions designed using an existing method, we confirmed that the proposed method can be appropriately used for designing the activation functions for the inference process of an FCM for clinical decision making.
This study dealt with only two kinds of functions and limited their adaption into an example of decision making with the designed knowledge model in other study. In future research, we will consider another type of functions such as hyperbolic tangent function and apply the functions to more various FCM models in medical field.
PDF Links
PubReader
XML Download
Full text via DOI
Full text via PMC
Download Citation
